Flash CS4から搭載された3次元表現の機能を、ActionScriptから制御する方法を習得するための入門講座です。
講師はロクナナワークショップの人気講座「 野中文雄の応用力に差をつけるActionScript数学講座 」を担当され、Adobe Flashデベロッパーセンター への寄稿、Flash解説書籍の執筆など、幅広く活躍されている 野中文雄(のなかふみお)氏です。
開催概要
- 日時:6月19日(金)13:00 – 16:15(開場12:30)
- 会場:東京・代々木「 TKP代々木ビジネスセンター 2号館 B1 」
- 講師:野中文雄(ロクナナワークショップ講師)
- 料金:4,800円(税込み)※学生料金(数量限定):2,400円(税込み)
ブログなどでご紹介いただく際のバナーをご用意いたしました。
イベントレポート

[野中文雄氏]
本イベントでは、ロクナナワークショップの人気講座「 野中文雄の応用力に差をつけるActionScript数学講座 」を担当され、Flash解説書籍の執筆など幅広く活躍されている 野中文雄 氏をゲストに、Flash CS4 Professionalより加わった3次元表現を可能にする3つのクラスとひとつのメソッドが紹介されました。
本稿では野中氏からの解説記事をご紹介します。
解説記事
※サンプルファイル ダウンロード(Flash CS4形式/約328KB)
01:3次元座標空間の表現
Flash Player 10では、3次元の表現ができるようになった。これは、3次元空間のオブジェクトを2次元のスクリーンに投影するときの遠近法、いわゆる「 パースペクティブ 」(perspective)が採入れられたことを意味する。具体的には、奥行きが遠ざかるほど、物体は小さく、間隔は狭く表現する。
たとえば、Flash CS4 Professionalで、タイムラインに配置した長方形のインスタンスをY軸で[3D回転]させると、奥の辺が短くなって台形として表示される(図001)。
![図001■インスタンスをY軸で[3D回転]させる](http://event.67.org/wps/2009/06/img_matrix2009_re0021.jpg)
図001■インスタンスをY軸で[3D回転]させる
コンピュータグラフィックスでこのような表現をする場合、画像を複数の三角形に分けて、それぞれを変形してからつなぎ合わせるのが通常だ。もちろん、Flash Player 10/ActionScript 3.0では、インスタンスに3次元の設定を加えれば、パースペクティブは自動的に与えられる。しかし、必要があればその三角形分割による変形の機能を利用できるように、ActionScript 3.0のGraphicsクラスにメソッドがひとつ加えられた。
この機能を用いると、矩形などの平面に3次元の凹凸を加えたかのような表現ができる(図002)。なお、分割した三角形に面として設定する画像は「テクスチャ」ともいい、それぞれの三角形にテクスチャを貼りつける操作は「マッピング」と呼ばれる。
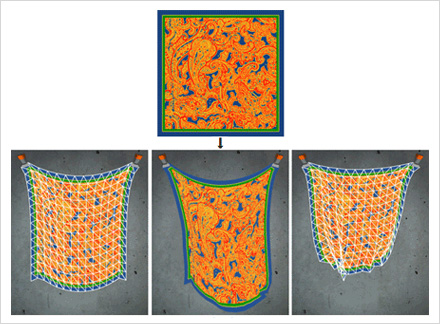
図002■矩形を分割した三角形にテクスチャマッピングして3次元の凹凸を表現する
02:Graphics.drawTriangles()メソッド
複数の三角形を描いて、それぞれに塗りを変形して適用するのが Graphics.drawTriangles()メソッドだ[*1]。テクスチャを複数の三角形に分割して、変形したうえで合成することにより、3次元を2次元に投影できる。まずは、 Graphics.drawTriangles()メソッドのシンタックスを確認しよう。
drawTriangles(頂点座標:Vector.<Number>, 頂点番号:Vector.<int> = null, uvtデータ:Vector.
<Number> = null):void 3つの引数には、分割する三角形の頂点座標や頂点番号、テクスチャのマッピングの仕方(uvtデータ)などの情報を指定する。分割する三角形の数を増やせば、複雑で多彩な表現ができる(前掲図002参照)。
メソッドの3つの引数は、データ型がFlash Player 10から備わったVectorクラスで定義されている。インスタンスの生成やデータ型の指定が少し変わっているので、先に簡単に説明しておこう。
Vectorクラス
Vectorクラスは、いわば最適化されたArrayクラス(配列) だ。Vectorインスタンスには、配列と同じように、複数の値にインデックスをつけて納められる。配列と違うのは、第1にエレメントに対して、データ型をひとつだけ指定する。そして第2に、エレメントのインデックスは連番でなければならない。
VectorクラスがArrayクラスと異なる点
1. エレメントのデータ型をひとつだけ指定。
2. エレメントのインデックスは連番。
Vectorクラスのコンスラクタメソッドは、以下のシンタックスでインスタンスを生成する。コンストラクタの後のドット(.)に続けて、山括弧<>の中にエレメントのデータ型(「ベース型」)を指定する。
Vector.<データ型>(長さ:uint = 0, 長さの固定:Boolean = false) インスタンスを代入する変数宣言のデータ型にも、山括弧<>でベース型を指定する。たとえば、変数myVectorにベース型が整数(int型)のVectorインスタンスを代入するのは、つぎのようなステートメントだ。
var myVector:Vector.<int> = new Vector.<int>(); Vectorインスタンスのエレメントにアクセスするには、配列と同様に配列アクセス演算子[]を用いる。また、Arrayクラスと同じく、 Vector.lengthプロパティやVector.push()メソッドなども備えている。
塗りのビットマップの指定
Graphics.drawTriangles()メソッドで三角形にテクスチャマッピングするには、 Graphics.beginBitmapFill()メソッドで塗りのビットマップを指定しなければならない。第1引数には、塗りに用いるビットマップのインスタンスを渡す。
beginBitmapFill(ビットマップ:BitmapData):void メソッドの第1引数には、[ライブラリ]のビットマップを指定することができる。そのビットマップには、[ビットマッププロパティ]ダイアログボックスで[クラス]に任意の名前を設定する(図003)。
![図003■[ビットマッププロパティ]ダイアログボックスで[クラス]を入力](http://event.67.org/wps/2009/06/img_matrix2009_re0041.jpg)
図003■[ビットマッププロパティ]ダイアログボックスで[クラス]を入力
Graphics.beginBitmapFill()メソッドの引数に渡すのは、BitmapDataインスタンスだ。[ライブラリ]のビットマップは、デフォルトで[基本クラス]としてBitmapData クラスを継承する(図002)。よって、ビットマップのインスタンスを生成するには、[クラス]に入力したクラス名(Pen)をコンストラクタメソッドとして、以下のようにnew演算子で呼出す。なお、コンストラクタの引数には、幅と高さを意味するふたつの数値を指定する。値はともに0でよい。
var myTexture:BitmapData = new Pen(0, 0); // ふたつの0を引数として渡す
mySprite.graphics.beginBitmapFill(myTexture); // メソッドにBitmapDataインスタンスを渡す 生成したビットマップ(データ型はBitmapDataで指定)のインスタンスは、 Graphics.beginBitmapFill()メソッドに引数として渡す。メソッドは、塗りの対象となるインスタンスのSprite.graphicsプロパティを参照して呼出す。これで、Spriteインスタンス(mySprite)への描画の塗りとして、ビットマップ(BitmapDataインスタンス)が設定された。あとは、Spriteインスタンスに描画メソッドでシェィプを描けば、その塗りにビットマップが適用される。
Graphics.drawTriangles()メソッドの引数
前述のとおり、Graphics.drawTriangles()メソッドには、3つのVectorインスタンスを引数として指定する。
Graphicsインスタンス.drawTriangles(頂点座標, 頂点番号, uvtデータ) ここでGraphics.drawTriangles()メソッドを用いて、たとえば正方形の画像の右下隅を少し引き伸ばすとしよう(図004)。簡単な変形なので、ビットマップはひとつの対角線でふたつの三角形に分ける。

図004■Graphics.drawTriangles()メソッドでビットマップを変形する
Graphics.drawTriangles()メソッドの第1引数は、変形した三角形の頂点の座標だ。今回は下図005のように、4頂点でふたつの三角形を組合わせる。引数として渡すVectorインスタンスには、4頂点のxy座標で計8つの数値をエレメントとして納める。
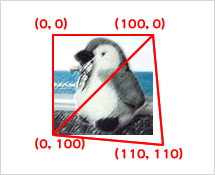
図005■第1引数は変形した三角形の頂点のxy座標
Graphics.drawTriangles()メソッドの第3引数には、三角形にマッピングするテクスチャの頂点の座標を、第1引数の座標に対応する順序で指定する。ただし、座標値は左上隅が原点(0, 0)で、右下隅を(1, 1)とする比率で表す(図006)。また、ふたつの値はuとvで示し、uv座標と呼ばれる。引数に渡すVectorインスタンスには、第1引数と同じ数の数値のエレメントが納められる。

図006■第3引数はマッピングするテクスチャの頂点のuv座標
ここで、三角形の頂点には、0から始まる整数の連番を頂点番号として下図007のように定めておく。すると、今回試そうとしているテクスチャマッピングでは、 Graphics.drawTriangles()メソッドに下表001の座標値を、それぞれ第1引数と第3引数に指定すべきことになる。

図007■頂点に0から始まる整数の連番を定める
表001■Graphics.drawTriangles()メソッドの第1引数/頂点座標と第3引数/uvtデータ
| 頂点番号 | 第1引数/頂点座標 | 第3引数/uvtデータ |
|---|---|---|
| 0 | (0, 0) | (0, 0) |
| 1 | (100, 0) | (1, 0) |
| 2 | (0, 100) | (0, 1) |
| 3 | (110, 110) | (1, 1) |
もっとも、これらの値だけでは、どの頂点で三角形が構成されるのかわからない。そこで、Graphics.drawTriangles()メソッドの第2引数は、三角形の3つの頂点番号の組を、分割した三角形の数だけ指定する。今回は、ふたつに分けた三角形の左上半分の頂点(0, 1, 2)と、右下半分の頂点(1, 2, 3)の計6つの整数を、Vectorインスタンスに納めて引数とすることになる。
さて、以上のとおりVectorインスタンスの引数3つを指定して、 Graphics.drawTriangles()メソッドによりテクスチャをマッピングするフレームアクションが以下のスクリプト001だ。Vectorインスタンスに納める値は、わかりやすいように座標あるいは頂点番号の組ごとに、Vector.push()メソッドで分けて加えている。[ムービープレビュー]を確かめると、テクスチャの右下隅が水平および垂直方向に10ピクセルずつ引き伸ばされてマッピングされる(図008)。
スクリプト001■Graphics.drawTriangles()メソッドでテクスチャをマッピング
// タイムライン: メイン
// 第1フレームアクション
var mySprite:Sprite = new Sprite();
var myGraphics:Graphics = mySprite.graphics;
var myTexture:BitmapData = new Pen(0, 0);
// 頂点座標のVectorインスタンス生成
var vertices:Vector.<Number> = new Vector.<Number>();
// 頂点番号のVectorインスタンス生成
var indices:Vector.<int>= new Vector.<int>();
// uvtデータのVectorインスタンス生成
var uvtData:Vector.<Number> = new Vector.<Number>();
addChild(mySprite);
// 三角形の頂点座標を加える(第1引数)
vertices.push(0, 0); // 頂点0
vertices.push(100, 0); // 頂点1
vertices.push(0, 100); // 頂点2
vertices.push(110, 110); // 頂点3
// 三角形の頂点番号の組合わせを加える(第2引数)
indices.push(0, 1, 2); // 左上半分: 頂点0-1-2
indices.push(1, 2, 3); // 右下半分: 頂点1-2-3
// テクスチャマッピングのuv座標を加える(第3引数)
uvtData.push(0, 0); // 頂点0
uvtData.push(1, 0); // 頂点1
uvtData.push(0, 1); // 頂点2
uvtData.push(1, 1); // 頂点3
myGraphics.beginBitmapFill(myTexture);
myGraphics.drawTriangles(vertices, indices, uvtData); 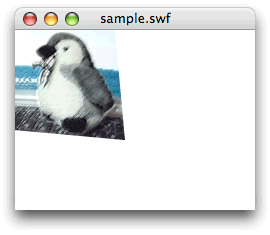
図008■変形した三角形にマッピングされたテクスチャ
ドラッグで変形した任意の四角形にテクスチャマッピング
Graphics.drawTriangles()メソッドの使い方が確かめられたので、簡単な応用例を紹介しよう。矩形のインスタンスの4隅にドラッグできるポイントを置き、それらの位置に合わせて変形した四角形にテクスチャをマッピングする(図009)。
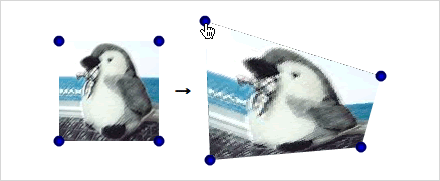
図009■ドラッグした4隅のポイントに合わせて変形した四角形にテクスチャマッピング
準備として、矩形のインスタンスの4隅に置くシンボルには、ドラッグできるようにフレームアクションを記述しておく。その中で、ドラッグしている間、メインタイムラインの関数xTransform()を呼出すようにする(図010)[*2]。メインタイムラインに定義する関数xTransform()の本体で、ドラッグした4隅のインスタンスの位置に合わせてテクスチャマッピングしようという訳だ。
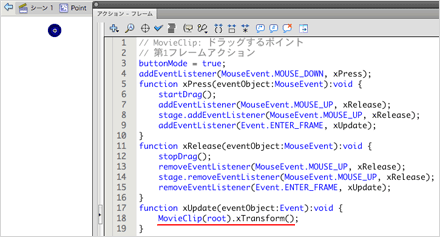
図010■ドラッグするシンボルに記述したフレームアクション
4隅のドラッグにより変わる値は、Graphics.drawTriangles()メソッドの第1引数であるマッピング対象の座標だけだ。第2および第3引数の値は、そのままでよい。すると、関数xTransform()では、第1引数のVectorインスタンスを作成し、それを渡してGraphics.drawTriangles()メソッドを呼出すことになる。なお、ドラッグする4隅のインスタンスには、矩形インスタンスの頂点座標に合わせて、point0_mc〜point3_mcと名前をつけた。また、Graphics.drawTriangles()メソッドに渡す第2引数と第3引数のVectorインスタンスは、それぞれ変数indicesおよびuvtDataに設定されているものとする。
function xTransform():void {
// 三角形の頂点座標(第1引数)
var vertices:Vector. = new Vector.();
vertices.push(point0_mc.x, point0_mc.y);
vertices.push(point1_mc.x, point1_mc.y);
vertices.push(point2_mc.x, point2_mc.y);
vertices.push(point3_mc.x, point3_mc.y);
myGraphics.beginBitmapFill(myTexture);
myGraphics.drawTriangles(vertices, indices, uvtData);
} Spriteインスタンスの生成や、Graphics.drawTriangles()メソッドに渡す第2引数と第3引数のVectorインスタンスの初期化については、前掲スクリプト001と基本的に同じでよさそうだ。したがって、ドラッグで変形した任意の四角形にテクスチャマッピングするフレームアクションは、つぎのスクリプト002のようになる。
スクリプト002■ドラッグで変形した任意の四角形にテクスチャマッピングするフレームアクション
// タイムライン: メイン
// 第1フレームアクション
var mySprite:Sprite = new Sprite();
var myGraphics:Graphics = mySprite.graphics;
var myTexture:BitmapData = new Pen(0,0);
var indices:Vector. = new Vector.();
var uvtData:Vector. = new Vector.();
addChildAt(mySprite, 0);
// 三角形の頂点番号の組合わせ(第2引数)
indices.push(0,1,2);
indices.push(1,3,2);
// テクスチャマッピングのuv座標(第3引数)
uvtData.push(0,0);
uvtData.push(1,0);
uvtData.push(0,1);
uvtData.push(1,1);
xTransform(); // ドラッグ前にテクスチャを初期位置にマッピング
function xTransform():void {
// 三角形の頂点座標(第1引数)
var vertices:Vector. = new Vector.();
vertices.push(point0_mc.x, point0_mc.y);
vertices.push(point1_mc.x, point1_mc.y);
vertices.push(point2_mc.x, point2_mc.y);
vertices.push(point3_mc.x, point3_mc.y);
myGraphics.clear(); // 描画を一旦消す
myGraphics.beginBitmapFill(myTexture);
myGraphics.drawTriangles(vertices, indices, uvtData);
} 新たに加えた処理が3つある。第1は、関数xTransform()の本体で、ビットマップの塗りを設定する(Graphics.beginBitmapFill()メソッドの)前にGraphics.clear()メソッドで前の描画を消したことだ。この処理がないと、前の塗りが残ってしまう(図011)。

図011■Grphics.clear()メソッドを呼出さないと前の描画が残る
第2に、SpriteインスタンスをDisplayObjectContainer.addChildAt()メソッドでタイムラインの表示リストに加えた。今回は、4隅のインスタンスを予めタイムラインに配置してある。DisplayObjectContainer.addChild()メソッドでSpriteインスタンスを加えると、それらの前面に表示されてしまう。そこで、 DisplayObjectContainer.addChildAt()メソッドの第2引数にインデックスとして0を渡すことにより、4隅のインスタンスの背面にSpriteインスタンスを配置した。
そして第3は、このフレームアクションからxTransform()関数を呼出したことだ。関数xTransform()は、4隅のインスタンスのいずれかをドラッグしなければ実行されない。つまり、そのままでは、ドラッグするまでタイムラインにビットマップが表示されなくなってしまうからだ。
[*1] Graphics.drawTriangles()メソッドについて詳しくは、Adobeデベロッパーセンターに寄稿した「三角形分割によるテクスチャマッピング - Graphics.drawTriangles()メソッド Part 1」および「角形分割によるテクスチャマッピング - Graphics.drawTriangles()メソッド Part 2」で解説している。
[*2] シンボルのフレームアクションは本題からそれるので、これ以上の説明は省く。具体的な内容は、サンプルファイルを見てほしい。
03:Matrix3Dクラス
Matrix3Dクラスを使うと、DisplayObejctインスタンスを3次元空間で座標変換できる[*3]。Matrix3DオブジェクトはTransformクラスにプロパティとして備わっており、DisplayObject.transformプロパティからアクセスする。インスタンスの座標変換というのは、具体的には平行移動や拡大・縮小、回転などを指す。
変換のprependとappend
Matrix3Dクラスによる平行移動や拡大・縮小、回転といった座標変換には、次表002のようなメソッドを用いる。各変換について、前に適用する(prepend)メソッドと後に適用する(append)メソッドがそれぞれ用意されている。
表002■Matrix3Dクラスの移動/拡大・縮小/回転のメソッド
| 変換 | 変換を前に適用するメソッド | 変換を後に適用するメソッド |
|---|---|---|
| 平行移動 | Matrix3D.prependTranslation() | Matrix3D.appendTranslation() |
| 拡大・縮小 | Matrix3D.prependScale() | Matrix3D.appendScale() |
| 回転 | Matrix3D.prependRotation() | Matrix3D.appendRotation() |

図012■Matrix3Dクラスの平行移動(左)/拡大・縮小(中央)/回転(右)のメソッドの変換結果
座標変換を前(prepend)に適用するか、後(append)に適用するかの意味と、互いの違いについて、回転を例にとって解説しよう。
Matrix3D.prependRotation()メソッド
Matrix3D.prependRotation()メソッドのシンタックスは、つぎのとおりだ。第1引数に、回転の角度を度数で渡す。そして第2引数には、回転の軸を指定する。xyz軸は、それぞれVector3Dクラスの定数Vector3D.X_AXIS、Vector3D.Y_AXIS、Vector3D.Z_AXISを用いる。
prependRotation(度数角:Number, 回転軸:Vector3D):voidマウスポインタの水平座標に応じた速さで、インスタンスをy軸で回転するフレームアクションが以下のスクリプト003だ。回転するインスタンスmy_mcは、予めタイムラインに配置しておく。
スクリプト003■3次元座標空間におけるインスタンスをy軸で回転させる
// タイムライン: メイン
// 第1フレームアクション
var nX:Number = my_mc.x;
var nDeceleration:Number = 0.3; // 回転スピードの調整係数
my_mc.z = 0; // 3次元座標のプロパティを操作
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = (mouseX - nX)*nDeceleration;
// 3次元座標空間においてy軸でインスタンスを回転
my_mc.transform.matrix3D.prependRotation(nRotationY, Vector3D.Y_AXIS);
} ひとつ注意しなければならないのは、デフォルトでは DisplayObject.transformプロパティにTransform.matrix3Dプロパティの値、つまりMatrix3Dオブジェクトが存在しない(nullになる)ことだ。DisplayObjectインスタンスに何らかの3次元座標の操作を加えて初めて、Matrix3Dオブジェクトが生成される。そのため、前掲スクリプト003では、DisplayObject.zプロパティに0(デフォルト値)を設定している。
[ムービープレビュー]を見ると、インスタンスはマウスポインタの水平座標がその基準点から離れるほど、y軸を中心として水平方向に速く回転する(図013)。
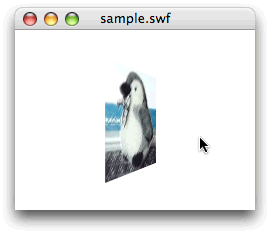
図013■インスタンスがマウスポインタの位置に応じた速さで水平に回転
Matrix3D.appendRotation()メソッド
前掲スクリプト003のリスナー関数xRotate()で、回転するメソッドを Matrix3D.appendRotation()に変えてみよう。メソッドのシンタックスは、基本的にMatrix3D.prependRotation()メソッドと同じだ。
appendRotation(度数角:Number, 回転軸:Vector3D):void 書替えてみると、インスタンスは自身の基準点ではなく、配置されたタイムラインの基準点を原点として回るようになる。つまり、メインタイムラインに配置したインスタンスをy軸で回転すれば、ステージ左端を軸に回ってしまう(図014)。
function xRotate(eventObject:Event):void {
var nRotationY:Number = (mouseX - nX)*nDeceleration;
my_mc.transform.matrix3D.appendRotation(nRotationY, Vector3D.Y_AXIS);
}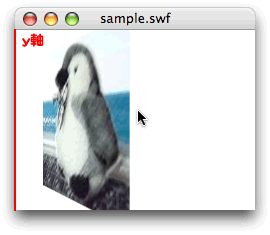
図014■インスタンスがステージ左端をy軸として回転する
実は、座標変換は、つねに配置された親タイムラインの基準点を原点として行われる。それは、Matrix3D.prependRotation()メソッドの場合も同じだ。しかし、ふたつのメソッドで回転する原点が異なる結果となったのは、変換の適用される順序が異なるからである。
座標変換が適用される順序
インスタンスのもつMatrix3Dオブジェクトに、引数なしで呼出したコンストラクタにより生成したMatrix3Dインスタンスを設定すると、座標変換が加えられる前のデフォルトの状態に戻すことができる。それは、位置が親タイムラインの基準点、サイズは原寸(水平100%×垂直100%)、回転なし(0度)となる(図015)。
my_mc.transform.matrix3D = new Matrix3D()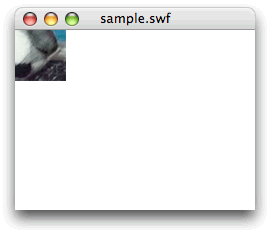
図015■インスタンスのデフォルト状態は位置が親タイムラインの基準点
インスタンスのDisplayObject.transformプロパティがMatrix3Dオブジェクト(Transform.matrix3Dプロパティの値)をもつとき、Flash PlayerはDisplayObjectインスタンスにそのMatrix3Dオブジェクトを適用してステージに表示する。
変換を前(prepend)に適用するメソッドというのは、このMatrix3Dオブジェクトより先に、インスタンスのデフォルト状態に対して実行される。デフォルトでは、インスタンスと親タイムラインの基準点が一致している。したがって、親タイムラインの基準点を原点として変換しても、インスタンスの基準点で行ったのと同じ結果になる。
変換を後(append)に適用するメソッドは、Matrix3Dオブジェクトが適用されてインスタンスが現行の状態になってから実行される。すると、座標変換は、インスタンスの基準点とは異なる親タイムラインの基準点を原点として適用される。
前掲スクリプト003のリスナー関数xRotate()で、 Matrix3D.appendRotation()メソッドを使って Matrix3D.prependRotation()と同じ処理にすることもできる。その場合、変換の適用順序をはっきりと変えてしまえばよい。
function xRotate(eventObject:Event):void {
var nRotationY:Number = (mouseX - nX)*nDeceleration;
var myMatrix3D:Matrix3D = my_mc.transform.matrix3D; // もとのMatrix3Dオブジェクトを保持
my_mc.transform.matrix3D = new Matrix3D(); // デフォルト状態に戻す
my_mc.transform.matrix3D.appendRotation(nRotationY, Vector3D.Y_AXIS); // 回転を先に適用
my_mc.transform.matrix3D.append(myMatrix3D); // もとのMatrix3Dオブジェクトを適用
} なお、Matrix3D.append()メソッドは、引数のMatrix3Dオブジェクトを後からインスタンスに適用して変換する。
append(後から適用する変換:Matrix3D):void 複数の座標変換を組合わせる
前に適用(prepend)する変換の方が、扱いは簡単だ。しかし、変換を組合わせたとき、細かな調整はしづらい。たとえば、スクリプト003に、マウスポインタの垂直方向の動きに対するx軸の回転を加えてみる。
var nX:Number = my_mc.x;
var nY:Number = my_mc.y;
var nDeceleration:Number = 0.3;
my_mc.z = 0;
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = (mouseX - nX)*nDeceleration;
var nRotationX:Number = (mouseY - nY)*nDeceleration;
my_mc.transform.matrix3D.prependRotation(nRotationY, Vector3D.Y_AXIS);
my_mc.transform.matrix3D.prependRotation(nRotationX, Vector3D.X_AXIS);
} [ムービープレビュー]で確かめると、マウスポインタの水平方向と垂直方向両方の動きに応じて回転の向きと速さが変わる。しかし、回転の方向が不自然だ。 Matrix3D.prependRotation()メソッドは、インスタンスのデフォルト状態に回転の変換を加える。そのため、タイムライン上でインスタンスがどの向きになっているかにかかわらず、インスタンスのx軸とy軸で回転してしまうからだ。

図016■マウスポインタを垂直に動かすとインスタンスのx軸で回転
後に適用(append)する変換であれば、向きは変えずに位置だけを親タイムラインの基準点に動かすことができる。そこで回転を加えたうえで、位置をもとの座標に戻せばよい。後から適用する平行移動には、 Matrix3D.appendTranslation()メソッドを用いる。引数にはxyz座標値を渡す(スクリプト004)。
appendTranslation(x:Number, y:Number, z:Number):void スクリプト004■3次元座標空間におけるインスタンスをx軸とy軸で回転させる
// タイムライン: メイン
// 第1フレームアクション
var nX:Number = my_mc.x;
var nY:Number = my_mc.y;
var nDeceleration:Number = 0.3;
my_mc.z = 0;
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = (mouseX - nX)*nDeceleration;
var nRotationX:Number = (mouseY - nY)*nDeceleration;
// 3次元座標空間でインスタンスを回転
my_mc.transform.matrix3D.appendTranslation(-nX, -nY, 0);
my_mc.transform.matrix3D.appendRotation(nRotationY, Vector3D.Y_AXIS);
my_mc.transform.matrix3D.appendRotation(nRotationX, Vector3D.X_AXIS);
my_mc.transform.matrix3D.appendTranslation(nX, nY, 0);
} Spriteインスタンスに6面で立方体を作成したMatrix3Dクラスの応用サンプル(adv_Matrix3D_cube.fla)でも、基本的に同じ処理内容で3次元空間における回転を行っている(図017)。ただし、関数はふたつに分け、マウスポインタの座標に応じた回転の向きと速さをrotateCube()で計算し、Spriteインスタンスとそれらの値を引数にしてrotateSprite()で回転させている。

図017■立方体をx軸とy軸で回転
Matrix3D応用サンプル■立方体の回転の処理
var nX:Number = stage.stageWidth / 2;
var nY:Number = stage.stageHeight / 2;
var nSensitivity:Number = 0.2;
var cubeSprite:Sprite = new Sprite(); // 中に別途立方体を作成
function rotateCube(eventObject:Event):void {
var nRotationX:Number = -(mouseY - nY) * nSensitivity;
var nRotationY:Number = (mouseX - nX) * nSensitivity;
rotateSprite(cubeSprite, nRotationX, nRotationY);
}
function rotateSprite(mySprite:Sprite, nRotationX:Number, nRotationY:Number):void {
var myMatrix3D:Matrix3D = mySprite.transform.matrix3D;
myMatrix3D.appendTranslation(-nX, -nY, 0);
myMatrix3D.appendRotation(nRotationX, Vector3D.X_AXIS);
myMatrix3D.appendRotation(nRotationY, Vector3D.Y_AXIS);
myMatrix3D.appendTranslation(nX, nY, 0);
} [*3] Matrix3Dクラスについては、併せてAdobeデベロッパーセンターに寄稿した「Matrix3Dクラス - 変換行列2」も参考にしてほしい。
04:Vector3Dクラス
Vector3Dクラスは、3次元空間の座標やベクトルを表し、その処理をするために用いられる[*4]。ベクトルとは、幾何学的には向きと大きさをもった値をいう。ここでは、ベクトルの内積と透視投影について説明する。
ベクトルの内積
ベクトルの内積を計算すると、ふたつのベクトルのなす角について調べられる。ベクトルAとBの内積はA・Bで表され、つぎの式により計算される。なお、絶対値|A|はベクトルAの大きさ(長さ)であり、θはベクトルAとBとのなす角を示す。
A・B = |A||B|cosθVector3D.dotProduct()を用いると、ふたつのVector3Dインスタンスの内積が求められる[*5]。内積の値が正負あるいは0かにより、ふたつのベクトルのなす角が鋭角・鈍角または直角か判別できる(表003)。
dotProduct(演算対象ベクトル:Vector3D):Number表003■ベクトルの内積となす角
| 内積の値 | なす角(θ) | cosθ |
|---|---|---|
| 正 | 90度より小さい(鋭角) | 正 |
| 0 | 90度(直角) | 0 |
| 負 | 90度より大きい(鈍角) | 負 |
内積を求める前掲の式|A||B|cosθで、ベクトルの絶対値は0以上なので、その積 |A||B|もまた0以上だ。したがって、cosθの値が、そのまま内積の値の正負または0かを決めることになる[*6]。cosθは(180度までの範囲では)、角度が90度未満なら正、90度のとき0、そして90度より大きければ負の値をとる(図018)。
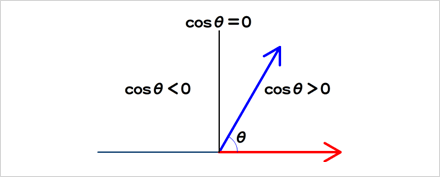
図018■内積の正負とベクトルのなす角度
前に紹介した回転する立方体のように閉じた立体については、背後の裏返った面は隠れて見えないので、表示する必要がない。そうした面は表示しないことで、描画の負荷を軽くできる。ふたつのベクトルとして視線(通常はz 軸の奥に向かうベクトル)と面の方向(面から垂直に正面に向かうベクトル)を考え、その内積を求めれば、視線に対して面が裏向きかどうかわかる。
以下のスクリプト005は、インスタンスのz座標を50ピクセル手前(-50)に移動し、z座標0(xy座標はインスタンスの基準点)を軸に水平回転させる。そのうえで、視線のベクトル(0, 0, 1)と面の方向(回転の中心から面の基準点まで)のベクトルで内積を計算し、裏返った面はアルファを50%(0.5)にして結果を確かめている(図019)。

図019■水平回転したインスタンスが裏返るとアルファは50%になる
スクリプト005■視線と面の方向のベクトルの内積で裏返った面を判定する
// タイムライン: メイン
// 第1フレームアクション
var nX:Number = my_mc.x;
var nY:Number = my_mc.y;
var nDeceleration:Number = 0.3;
var view:Vector3D = new Vector3D(0,0,1); // 視線のベクトル
var origin:Vector3D = new Vector3D(nX,nY,0); // 原点のベクトル
my_mc.z = -50;
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = (mouseX - nX)*nDeceleration;
var nRotationX:Number = (mouseY - nY)*nDeceleration;
my_mc.transform.matrix3D.appendTranslation(-nX, -nY, 0);
my_mc.transform.matrix3D.appendRotation(nRotationY, Vector3D.Y_AXIS);
my_mc.transform.matrix3D.appendTranslation(nX, nY, 0);
var myPosition:Vector3D = my_mc.transform.matrix3D.position;
var vector:Vector3D = myPosition.subtract(origin);
var nDotProduct:Number = view.dotProduct(vector);
if (nDotProduct > 0) {
my_mc.alpha = 0.5;
} else {
my_mc.alpha = 1;
}
} 新たなVector3Dインスタンスは、Vector3D()コンストラクタにxyz座標を引数に渡して生成する。z軸正方向の視線のベクトル(view)とインスタンスが回転する原点の位置ベクトル(origin)を、Vector3Dインスタンスとして初期化した。
回転するインスタンスは基準点を真ん中に定めたので、その位置ベクトル(myPosition)から原点のベクトル(origin)を差引けば、インスタンスの面の方向がベクトル(vector)として得られる。Vector3Dクラスは、ベクトルの引き算を Vector3D.subtract()メソッドとして備える。
subtract(差引くベクトル:Vector3D):Vector3Dなお、インスタンスのもつMatrix3Dオブジェクトからその基準点の位置ベクトルをVector3Dインスタンスとして得るには、Vector3D.positionプロパティを用いる。
視線のベクトル(view)とインスタンスの面の方向のベクトル(vector)との内積(nDotProduct)を求めれば、視線に対してインスタンスが表向きか裏向きかを確かめられる。内積の値が正のときは、インスタンスの面は裏返っている(前掲図018)。
Matrix3Dクラスの応用サンプルでも、基本的に同じ考え方によって立方体の裏側の面を非表示にしている。関数arrangeFaces()がその処理を担う。ただし、回転しているのは立方体のSpriteインスタンス(cubeSprite)であって、その中に組立てられた6面のSprite インスタンス自体は動かない。そこで、面のインスタンスの座標を、立方体が置かれたメインタイムラインから見た値に変換しなければならない。
Transform.getRelativeMatrix3D()メソッドは、インスタンスのMatrix3Dオブジェクトを、基準タイムラインの座標空間に変換する。なお、Matrix3D応用サンプルのVectorインスタンスfaces_vectorには、立方体の6面のSpriteインスタンスが納められている。
getRelativeMatrix3D(基準タイムライン:DisplayObject):Matrix3D Matrix3D応用サンプル■立方体の裏側の面を非表示にする処理
function arrangeFaces():void {
var faceSprite:Sprite;
var nLastIndex:int = cubeSprite.numChildren - 1;
var nLength:Number;
var i:uint;
var view:Vector3D = new Vector3D(0,0,1);
nLength = faces_vector.length;
for (i=0; i < nLength; ++i) {
faceSprite = faces_vector[i];
var myPosition:Vector3D = faceSprite.transform.getRelativeMatrix3D(this).position;
var vector:Vector3D = myPosition.subtract(cubeSprite.transform.matrix3D.position);
var nDotProduct:Number = view.dotProduct(myPosition);
if (nDotProduct > 0) {
faceSprite.visible = false;
} else {
faceSprite.visible = true;
}
}
} 透視投影
透視投影とは、3次元空間の座標を遠近法が適用された2次元平面に描画することをいう。3次元空間を考えたとき、視点から投影面への焦点距離と投影面からオブジェクトまでのz方向距離が投影像の大きさを決める(図020)。
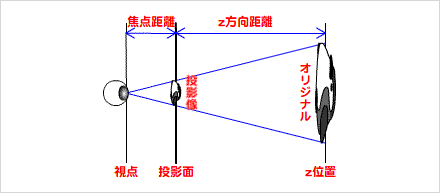
図020■透視投影を3次元空間の上から見たyz平面で考える
相似の三角形と辺の比の関係から、オリジナルの大きさと投影像の大きさの比は、つぎの式で表される。
投影像の大きさ/オリジナルの大きさ = 焦点距離/(焦点距離+z方向距離)
投影像の大きさ = オリジナルの大きさ×焦点距離/(焦点距離+z方向距離)Vector3D.project()メソッドは、Vector3D.wプロパティを用いて3次元座標を透視投影する。具体的には、xyz各座標値をVector3D.wプロパティの値で割り算する。
function project():void Vector3Dインスタンスは、4次元のベクトルとして表される(図021)。 Vector3D.wプロパティは、xyz座標に続くベクトルの4つ目の成分(要素)である。透視投影の変換比率にかぎらず、他のパラメータを設定して使うことも想定されているようだ。
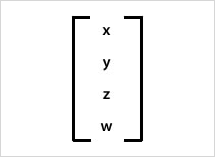
図021■Vector3Dクラスの列ベクトル表現
Vector3D.wプロパティに透視投影の変換比率を設定する場合、前述のとおり Vector3D.project()メソッドはこの値でVector3Dインスタンスのxyz座標値を除する。したがって、プロパティにはつぎの式の値を設定すべきことになる。
Vector3D.wプロパティ = (焦点距離 + Vector3D.zプロパティ値)/焦点距離Vector3Dクラスの応用サンプル(adv_Vector3D_cube.fla)では、立方体の8頂点座標のみをVector3Dクラスで管理し、回転した頂点を2次元座標に透視投影したうえで、2次元の描画メソッドによりワイヤーフレームを描いた(図022)。関数 xGetProjectedPoints()では、透視投影の変換比率をVector3D.wプロパティに設定して、Vector3d.project()メソッドで透視投影している。そして、この関数は2次元に投影した頂点のxy座標をPointインスタンスにして、それらが納められた配列を戻り値として返す。
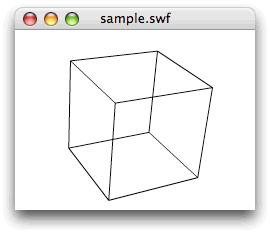
図022■Vector3Dインスタンスの頂点座標を透視投影してワイヤーフレームを描画
Vector3D応用サンプル■Vector3Dインスタンスの3次元座標をVector3d.project()メソッドで透視投影
function xGetProjectedPoints(myVertices:Vector.<Vector3D>):Vector.<Point> {
var nLength:uint = myVertices.length;
var projectedPoints:Vector.<Point> = new Vector.<Point>();
for (var i:int = 0; i<nLength; i++) {
var myVector:Vector3D = myVertices[i];
var cloneVector:Vector3D = myVector.clone();
cloneVector.w = (focalLength+myVector.z)/focalLength;
cloneVector.project();
projectedPoints.push(new Point(cloneVector.x, cloneVector.y));
}
return projectedPoints;
} Vector3D.project()メソッドでひとつ注意しておかなければならないのは、参照したVector3Dインスタンスのxyz座標値を書替えてしまうことだ。もとの3次元空間の座標値を保持しておくためには、Vector3Dインスタンスを複製して、その複製にメソッドを適用する必要がある。Vector3D.clone()メソッドは、Vector3Dインスタンスを複製して、その新しいVector3Dインスタンスを返す。
clone():Vector3DMatrix3Dクラスを用いたVector3Dの座標変換
Matrix3Dクラスとの関わりで、ひとつ補足しておく。 Matrix3D.transformVector()メソッドを用いると、Vector3Dインスタンスの座標をMatrix3Dオブジェクトにより変換できる。メソッドには引数として、変換対象となるVector3Dインスタンスを渡す。
transformVector(変換対象べクトル:Vector3D):Vector3D Vector3Dクラスの応用サンプルでは、関数xTransform()で Matrix3D.transformVector()メソッドによりVector3Dインスタンスに座標変換を加えた。Vector3DインスタンスはMatrixオブジェクトをもたないので、新たなMatrix3Dインスタンスを生成したうえで、回転の変換を与え、Vector3Dインスタンスに適用している。
Vector3D応用サンプル■Vector3DインスタンスにMatrix3D.transformVector()メソッドで回転の変換
function xTransform(myVertices:Vector.<Vector3D>, speed:Point):void {
var myMatrix:Matrix3D = new Matrix3D();
myMatrix.appendRotation(speed.x, Vector3D.Y_AXIS);
myMatrix.appendRotation(speed.y, Vector3D.X_AXIS);
var nLength:uint = myVertices.length;
for (var i:int = 0; i<nLength; i++) {
myVertices[i] = myMatrix.transformVector(myVertices[i]);
}
} [*4] 併せて、「 Vector3Dクラス 」を参照してほしい。
[*5] Vector3D.dotProduct()メソッドおよび内積について詳しくは、「 Vector3D.dotProduct()メソッド 」をお読みいただきたい。
[*6] cosなどの三角関数の意義については、AdobeのTechNote「 角度と座標の計算 - Flash の三角関数を使う 」が参考になる。
(2009/6/20 野中文雄)


